论文总字数:8203字
目 录
摘要 1
Abstract 2
1前言 3
2用欧拉积分推导出斯特林公式 4
3斯特林公式的证明 9
3.1用数项级数及含参量积分等证明 9
3.2利用Wallis公式结合图形面积证明 11
4 斯特林公式的应用 14
4.1斯特林公式的一些简单应用 14
4.2斯特林公式在采样定理中的应用 15
5小结 18
6讨论 19
参考文献 19
致谢 20
斯特林公式的证明与应用
张晨
,China
Abstract: As we all know, Stirling's formula is a mathematical estimation formula that used to calculate the approximate value of n factorial. This paper gives a simple method to prove this formula and Wallis formula combined with graphic area is used to prove it in this paper. We intend to understand and master the ingenuity of Stirling's formula through the study of it, so that it can be applied and generalized in statistics and mathematical analysis, as well as in the Lemma proof of sampling theorem.
Key words: Stirling formula; Shannon’s sampling theorem; Local average sampling ;Wallis formula
1前言
我们知道斯特林公式是用来求n的阶乘近似值的估计公式。关于该公式计算的讨论由来已久,我们能追溯到法国数学家棣美弗,他最早在《分析杂论》中,发现了正态分布,并由此给出了该公式的表达形式:

后来由苏格兰的J.斯特林,他证明了上面公式中的常数,其值是 ,即得到现在常用形式:
,即得到现在常用形式:

推广到更加精确的形式是:

或者也可以写成:

斯特林公式是用来估计当n充分大时,n!的近似值。斯特林公式形式为:

也可以简写成:

由上面形式可以看出,斯特林公式其实是一个关于阶乘的估计式。
在证明方面,由[1]中可知,在概率论中的一些定理证明及例题中遇到阶乘计算时会使用斯特林公式,并且费勒在[2]中比较详尽地探讨了斯特林公式在概率论中的应用。国内外的学者主要通过两个角度证明这个该公式,一是数学分析的角度,通过一些积分、级数、展开等等方法,这种方法技巧性略高,过程也略微复杂,例如在[9]中,张志军给出了一种初等证明,即利用数项级数、泰勒展开等方法证明,看似简单,但是每一步的又来并不明显,过于技巧化。另一个角度则是通过概率论的角度,利用一些分布函数、Poisson分布以及 分布等方法证明该公式。总而言之,其就是用来估计
分布等方法证明该公式。总而言之,其就是用来估计 近似值的数学公式,因此它的证明方法、技巧类型也五花八门。
近似值的数学公式,因此它的证明方法、技巧类型也五花八门。
再说应用方面,高钺在[5]中利用斯特林公式证明了统计学的重要结论,即 分布的极限分布为正态分布,体现该公式在概率论证明的优越性;马凤昌在[8]中除了证明斯特林公式外还给出了其高精度误差估计公式,它的误差估计对于实际的理论应用,例如物理、通信等方面的测量值,由于一些不可避免的人为或是仪器误差,可以估计出更为精确的答案;例如[6]中,宋艳霞利用斯特林公式估计局部采样定理的截断误差并讨论局部平均时的收敛性,这个应用体现了斯特林公式在含有阶乘的定理以及误差估计等方面的重要作用。总而言之,除了在一些解题方面有着独有的优势之外,在实际问题的应用方面也有着深刻的作用。
分布的极限分布为正态分布,体现该公式在概率论证明的优越性;马凤昌在[8]中除了证明斯特林公式外还给出了其高精度误差估计公式,它的误差估计对于实际的理论应用,例如物理、通信等方面的测量值,由于一些不可避免的人为或是仪器误差,可以估计出更为精确的答案;例如[6]中,宋艳霞利用斯特林公式估计局部采样定理的截断误差并讨论局部平均时的收敛性,这个应用体现了斯特林公式在含有阶乘的定理以及误差估计等方面的重要作用。总而言之,除了在一些解题方面有着独有的优势之外,在实际问题的应用方面也有着深刻的作用。
最后,本文在以上文献的基础上,先介绍了由欧拉积分对斯特林公式的推导,接着给出了两种方法证明斯特林公式,最后在斯特林公式的应用方面,除了计算[4]中给出的一些数学分析的例题外,还将它运用于信息通信方面的一个定理的证明中,即利用斯特林公式和sinc的泰勒展开对香农采样定理的引理进行证明。
2用欧拉积分推导出斯特林公式
在研究欧拉积分时,我们得到表达式:
 (2.1.1)
(2.1.1)
任意整数 ,该式给出了n!的一个简单表达,而当n为大于-1的非整数时,该式可看成函数n!的定义。很大整数的阶乘是一个复杂的又不便估计的数值对象,因此当n非常大时,我们可以找出一个表示n!的既简单、又便于估计的近似表达式。(2.1.1)式虽然不能直接成为这种表达式,但可以从它出发,可导出n!的满足上述要求的近似公式。
,该式给出了n!的一个简单表达,而当n为大于-1的非整数时,该式可看成函数n!的定义。很大整数的阶乘是一个复杂的又不便估计的数值对象,因此当n非常大时,我们可以找出一个表示n!的既简单、又便于估计的近似表达式。(2.1.1)式虽然不能直接成为这种表达式,但可以从它出发,可导出n!的满足上述要求的近似公式。
(1)在(2.1.1)中,令 则可以得到:
则可以得到:

于是,我们可以得到:

(2)令 ,推出
,推出 的一些性质。
的一些性质。
又因为:

所以可知:当 时,
时, 递增;
递增;
当 时,
时, 递减;
递减;
在点x=0时, 有一极大值
有一极大值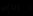 。
。
又因为 ,因此当
,因此当 时,函数
时,函数 恒为正,并且当
恒为正,并且当 时,它单调趋于0。
时,它单调趋于0。
其次有:

已知 的泰勒展开公式为:
的泰勒展开公式为:

其中,我们令 是一个取决于x的量,当
是一个取决于x的量,当 时,它是一个有界量。因此
时,它是一个有界量。因此


从而得到:
 (2.1.2)
(2.1.2)
又因为当 时,无穷小量
时,无穷小量 与t等价,得到:
与t等价,得到:

其中在 时保持有界。所以,如果n与x这样变化时:保持,则:
时保持有界。所以,如果n与x这样变化时:保持,则:

其中的 当
当 时,它是一个有界量。因此,当
时,它是一个有界量。因此,当 时,可得:
时,可得:

剩余内容已隐藏,请支付后下载全文,论文总字数:8203字


