论文总字数:6004字
目 录
摘要 1
Abstract 2
1引言 3
2预备定理 3
3新定义与新定理 4
4该类函数的衍生与推广 10
5展望与应用 11
参考文献 15
致谢 16
一类函数的渐近性质及其应用
李庆
,China
Abstract: In this paper, we first describe the definition of the slowly increasing function and the generalized slowly increasing function from zero to positive infinity, and then get the theorems related to the asymptotic properties of this kind of function, and further point out that this type of function approaches an exponential function at infinity; Secondly, we generalize the original zero-to-positive infinity slow growth function into the new zero-to-one interval. On the basis of the original, we have redefined slowly increasing function and the generalized at the zero-to-one interval,and obtained a great breakthrough, find that the function tends to be close to another function similar to the exponential function; in addition, I have obtained many important theorems and inferences on the basis of the previous research, which helps us understand this function in more easily.; In the end, this article has promoted from three perspectives: different quadrants, different change trends, and more general functions. So it has greatly inspired me.
Key words: slowly increasing function; generalized slowly increasing function; asymtotic property; new theorems
1引言
目前,在我们本科的学习阶段,最能表现函数渐近性质的便是函数的极限,即函数趋于某一特定点或者无穷区间时,函数的逼近值。除此之外,函数的渐近线也是描绘函数渐近性质另一外在辅助工具。周向宇曾在大学本科期间研究过这样一类函数 的渐近性质,这类函数满足这样一些条件:
的渐近性质,这类函数满足这样一些条件:
 ,
,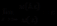 (
( )
)
最终发现这类函数有这样一个性质:
 . (1.1)
. (1.1)
不过我们很容易发现周向宇在他的文章中并没有完完全全阐述完,还有许多类似的性质和证明过程等待我们去补充的,这也就激发了我研究该类函数的极大的兴趣。
首先,周向宇研究的是区间 上的这类函数,然后我们便会去思考,倘若函数仅在区间
上的这类函数,然后我们便会去思考,倘若函数仅在区间 上有意义,我们该去怎样给其定义,这是本文的重中之重。
上有意义,我们该去怎样给其定义,这是本文的重中之重。
其次,周向宇研究的是类似于增函数的函数,那我是否可以从减函数方向研究;周向宇研究的是第一象限的函数,那我同样是否可以考虑其他象限。
抱着这些问题的思考,我开始了本文的写作。
2预备定理
定义2.1[1] 若 于
于 为正值连续函数,
为正值连续函数, 是单调递增函数,当
是单调递增函数,当 趋于无穷时
趋于无穷时 逼近于正无穷,并且存在一常数
逼近于正无穷,并且存在一常数 使得
使得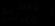 ,我们称满足该条件的这类函数为区间
,我们称满足该条件的这类函数为区间 上的缓增函数.
上的缓增函数.
定理2.1[1] 若 为区间
为区间 上的缓增函数,则有
上的缓增函数,则有
 . (2.1)
. (2.1)
不难知道,这是对于一个特殊的情形函数 对应所得的性质,所以可以将函数推广到更一般的情形.
对应所得的性质,所以可以将函数推广到更一般的情形.
定义2.2[1] 若 于
于 上为正值连续函数,当
上为正值连续函数,当 趋于无穷时
趋于无穷时 逼近于正无穷,并且存在一个常数
逼近于正无穷,并且存在一个常数 使得
使得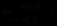 ,(其中
,(其中 为常数)我们称满足该条件的这类函数为区间
为常数)我们称满足该条件的这类函数为区间 上的广义缓增函数,不难知道
上的广义缓增函数,不难知道 .
.
定理2.2[1] 若 为区间
为区间 上的广义缓增函数,则有
上的广义缓增函数,则有
 . (2.2)
. (2.2)
显然,根据定理2.2的结果可以知道,定理2.1中函数 即使不是单调递增函数,但满足区间
即使不是单调递增函数,但满足区间 上的缓增函数的其他性质,定理3.1的结论仍然是成立的.
上的缓增函数的其他性质,定理3.1的结论仍然是成立的.
注 由定理3.2的结论 可知:
可知:
 ,
, ,当
,当 时,有
时,有

即有
 (2.3)
(2.3)
也就是
 . (2.4)
. (2.4)
因为 是任意的,令
是任意的,令 ,我们可以知道
,我们可以知道 .也就是说对于广义缓增函数
.也就是说对于广义缓增函数 来说,当
来说,当 足够大的时候,
足够大的时候, 的函数图像无限逼近于指数函数
的函数图像无限逼近于指数函数 .本节中以上两个定义以及两个定理是本文研究的基础,我们由个别到一般,由特殊到普遍,进而有了下文的讨论.
.本节中以上两个定义以及两个定理是本文研究的基础,我们由个别到一般,由特殊到普遍,进而有了下文的讨论.
3新定义与新定理
剩余内容已隐藏,请支付后下载全文,论文总字数:6004字


