论文总字数：15424字

目 录

1.引言 1

2.组合数学与数学竞赛的简介 1

2.1 组合数学 1

2.2 数学竞赛 2

3.学习组合数学的方法 2

4.组合数学的几种数学方法在数学竞赛中的应用 3

4.1 排列组合 3

4.2 抽屉原理 6

4.3 容斥原理 8

4.4 递推关系 9

参考文献 14

致谢 15

附录 16

组合数学在数学竞赛中的应用

马兆磊

摘要：数学竞赛，作为发掘数学人才的一种手段，在中学和大学越来越受到师生的喜欢。在内容上，数学竞赛中的组合数学大致可以分成两大类，组合设计问题和组合计数问题，我们在这里主要研究组合计数问题。组合数学的知识基础是加法原理和乘法原理；常用的组合数学方法有抽屉原理、容斥原理、排列组合和递推关系等等。

本文主要对组合数学的历史背景以及发展过程进行解说，通过几类数学竞赛中常见的组合数学问题进行解析研究，主要包括排列组合、抽屉原理、容斥原理、递推原理以及其他典型方法，并在排列组合中应用组合数学中的计数方法解决安卓手机九宫格解锁问题。

关键词：抽屉原理，容斥原理，排列组合，递推关系

Application Of Combinatorial Mathematics In Mathematics Competition

Ma Zhaolei

College of mathematics and statistics, Nanjing University of Information Science amp; Technology Nanjing Jiangsu

Abstract：Mathematics competition, as a mean of exploring mathematics talents, is more and more popular in teachers and students in middle schools and colleges. In the content, the mathematical contest in the combinatorial mathematics can be divided into two categories, the combinatorial design problems and combinatorial counting problems. We are here mainly to study combinatorial counting problems. The knowledge base of combinatorial mathematics are the addition principle and the multiplication principle, The common methods used in Combinatorial Mathematics are the principle of drawer, the principle of inclusion and exclusion, the permutation and combination, the recurrence relation and so on.

This paper mainly explains the historical background and development process of the combination of mathematics through analyzing and studying the common mathematical problems in several kinds of mathematical competitions , mainly including the arrangement and combination, the drawer principle, the principle of inclusion and exclusion, the recurrence principle and other typical methods, and uses the counting method in combinatorial mathematics to solve the mobile phone Android 33 Grids unlocking problems in permutations and combinations.

Key words： Drawer principle, inclusion-exclusion principle, permutations and combinations，recurrence relation

1.引言

组合数学问题有着悠久的历史，最早可以追溯到四千多年前，大雨治水的时候观察到乌龟身上的点集。中国的组合数学最早是在宋朝时候的贾宪三角，后来被我们称作杨辉三角。十六世纪中，德国著名数学家莱布尼茨给它命名为组合学，代表着新的学科产生。随着科技的飞速发展，组合数学在生产生活中存在的越来越广泛，成为一门不可或缺的知识体系，受到人们的欢迎，发展迅速。

数学问题的研究自然离不开解答问题，掌握数学知识的一个重要表现就是能够善于解答数学问题。本文主要先对组合数学和数学竞赛进行介绍，通过对数学竞赛中所占比重较大的组合数学问题进行分析解决，然后再在排列组合这块应用知识对我们日常生活中常见的安卓手机九宫格解锁的方法数进行分析解决。

2.组合数学与数学竞赛的简介

2.1 组合数学

组合数学有着悠久的历史，相传在大禹治水的时候，发现了一只乌龟，乌龟的背上有个奇特的点图，把这个点图的各个部分都用数字代替，就成了我们今天的三阶的数字方阵。这个方阵有一个特点，就是它的每一行、每一列、以及斜对角的三个数字的和都是15，这就是最早的组合数学问题。

生活和科学研究中也存在着无数的组合数学问题，因此组合数学应用的范围之广，生命力之顽强也可以看得出来。比如下面几类常见的问题：

（1）中国邮差问题：这个问题最初是由加管梅谷教授提出，其主要内容是根据邮递员在城市的各条路上送邮件，如何走才能使经过的路程最短？这个问题并不是一个NP完全问题，因为它存在着多项式复杂度算法：首先，要求出奇数点，用匹配算法来算出这些所经过的店之间的连接方式，最后再用欧拉公式算出结果。

（2）地图着色问题：在地图上为了区分不同国家，每个相邻国家就需要用不同的颜色来着色，那么只用四种颜色能否完成地图的着色呢？这就是著名的四色定理。四色定理最初提出虽然是跟地图染色工作工程有关系的，但是这个定理本身却是一个组合计数问题。很多人尝试着证明了四色问题并发表都被后人证明是出错的，直到1977年，数学家Wolfgang Haken 和Kenneth Appl借助电子计算机首次得到了完整的证明，四色问题也最终成为了我们现在的四色定理。

（3）哥尼斯堡七桥问题：两百年前有着这么一个问题：在一条河上存在着两个岛屿，岛上有四个部分可以由七个桥连接起来，试问能不能从每个桥上都走过并且每个桥只走一次？(如下图所示)

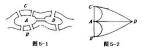
在18世纪中期，著名数学家欧拉成功的证明了这个问题，证明的结果是没有合适的方法。要想使得每座桥都走过并且只走一次，也就是看成图如左图所示，把复杂的问题简化成一个平面上四个点七条线的问题。欧拉采用了我们熟悉的抽象分析法，简化了此问题，这一方法在后来的用途也越来越广泛。

（4）组合数学问题与我们日常生活有着千丝万缕的关系，也就是说组合数学问题存在于生活中的方方面面，与我们息息相关。比如说这么一个有趣的组合数问题：小明一家要过桥，只有一个手电，桥上一次只能走两个人，小明过桥需要一分钟，弟弟过桥需要两分钟，爸爸过桥需要五分钟，妈妈过桥需要十分钟，爷爷过桥需要十五分钟，求问怎么样过桥用的时间最少？这个问题很有趣，先从两个极端入手，小明和弟弟的速度最快，妈妈和爷爷的速度最慢，这样的话我们可以先让小明带着弟弟过去，用时两分钟，然后小明回来或者弟弟回来，我们先假定小明回来，用了一分钟，那么重点来了，爷爷和妈妈一起过去，一共用了十五分钟，之后弟弟拿着灯回来，用了两分钟然后小明带着爸爸过去，用了五分钟，小明再回来用时一分钟，之后带着弟弟过桥用时两分钟，这样就做到了用时最短了，一共用时2 1 15 2 5 1 2=28分钟。

（5）组合数学在各类商业之中也有着重要的作用，比如我们大学师生大约有三万人左右，一年有365天，则平均每天大约有8个人一同过生日，说到过生日，必然有同学聚餐和买蛋糕之类的消费活动，对于蛋糕店来讲，可以在生日同一天的人一起定蛋糕优惠为亮点，收集师生生日，并与生日前期送来祝福，给与优惠种种，吸引顾客的要求，以此让生意越做越好。

2.2 数学竞赛

数学竞赛作为当代发现数学人才的一种手段，有着悠久的历史，是青少年的一种通过数学考试的智力竞赛。相对来讲比较正规的数学竞赛是从1894年，在匈牙利开始的，迄今为止已经举办了九十多届。我国早在战国时期就有齐威王与田忌赛马，也是一种对策论思想的比赛。数学竞赛在我国中学和大学越来越受到广大师生的重视，在数学竞赛的过程中，学生可以提升除了在课堂上学到的以外的知识，提升自己解题能力，老师也可以通过数学竞赛找到教学新目标新方法，发现数学人才，可以做到因材施教，让喜爱数学的学生可以更好的发展这方面的兴趣。

纵观数学竞赛题目，无论是初中高中又或者是大学竞赛，组合数学题目都有着相对较多的比重，这也体现了人们对组合数学的重视以及看好。组合数学对数学竞赛有着重要的意义，数学竞赛对于组合数学的学习也十分重要，二者相辅相成，相互促进，相互进步。

3.学习组合数学的方法

首先，组合数学作为数学题型的一种，有着数学的共性，也就是它的答题方法是多样的。对于同一种类型的题目，不同的人看法不同，理解思路不一样，其解的题思路也就会千差万别，但只要方法没有偏差，最终得到的结果或想要得到的东西是一样的。因此，在学习过程中我们不应该仅仅满足于接受书本上的解题思路，应该学会从不同的角度思考解决问题，用发散的思维接受新知识，在审题过程中能够从一个信息中得到多个隐藏条件，然后在应对不同的问题或者不同的问法时候才不至于无从下手。

其次，我们要学会分析解题的过程，要明白为什么这么想，或者说还能够用什么方法达到一样的效果，以防思维定势，我们要做到能够灵活的分析问题。因为在学习的过程中，一些人很有可能没有找到自己的学习方法，只能够根据书本或者老师的方法反复认知，时间久了就会造成思维定式的不好的影响，在解题过程中只会按照熟悉的方法或者规律解答问题，一旦遇到同一类的新题，换一种问法或者思路，就会发现之前的答题思路并不适用本题，就会感到无从下手，自然找不出答题办法。数学竞赛中的组合数学问题，很多情况下不会直接给出书上固定模式的题案，往往都会经过各种题型的变化和重装，虽然表面上看上去十分相似，但是真正解答起来却差别很大，这就需要抽丝剥茧，找出我们所需要的条件或者结论。我们还要敢于大胆的联想，根据之前的经验找出不同题目之间的相同之处和区别所在，然后把有关联的问题联系起来。

此外，无论是组合数学还是其他数学问题，都要明白学习是一个循序渐进的过程，任何问题我们都会从简单的学起，慢慢引申到相对来讲难理解一些的事例当中。因此，在学习的过程中，应该着重学习引申过程中难易问题之间的联系和差别，找到困难问题的本质，这样我们才能够更好的理解此类问题。因此，学习的过程也就是归纳总结的过程，边学边归纳，能够使的新旧知识构成一个学习的体系，我们接纳起来也会相对来讲容易的多。

很多数学题型来源于我们的日常生活并且应用于生活，所以我们要在学习过程中发现数学的规律，让自己能够感受到组合数学的魅力，这样也能够培养我们的自主学习的兴趣与能力，使我们在今后的学习解题过程中真正的做到得心应手。

4.组合数学的几种数学方法在数学竞赛中的应用

4.1 排列组合

排列组合是组合数学中较为基础的部分，其方法简单，但是用途却很广。排列^[2]就是指从一定个数的元素中取出指定个数的元素进行有序排列。组合^[2]则是指从一定个数的元素中取出指定个数的元素，但不需要考虑排序。

排列组合的应用主要从最基本的两个基本原理出发，也就是加法原理和乘法原理，再到不同元素的排列组合、圆排列、重复排列、多组组合和重复组合等等，组合数学是一门基础的知识点，许多竞赛题中解题会用到排列组合的知识，但并没有典型的竞赛题。在此，选几类组合数学的典型方法进行分析。其中的例1使用了排列组合中基本的加减法，例2使用了特殊值迭代法求解，两种方法虽然简单，但是其用处以及意义却很大。

例1.有多少个能被3整除而又含有数字6的五位数？

分析：五位数即从10000~99999共90000个数字，则有90000/3=30000个数字可以被3整除。之后再讨论其中含有6的个数，，又因为讨论每个位数含有6的个数，则有两个或两个以上位数同时含有6的情况出现，讨论结果会重复，所以我们可以讨论其对立面，即所以位上不含6的情况。我们先看最高位，最高位不能为0，也不能为6，因此有8种情况，即1,2,3,4,5,7,8,9这八种情况，同时在千位，百位，各位也不能出现6，则各位均有九种可能。我们先看前四位的和，假设前四位的和为，则 mod 3可以等于0或者1或者2，假设 mod 3的值为0，则个位可以取3，0,9；假设 mod 3的值为1，则个位可以取2,5,8；假设 mod 3的值为2，则个位可以取1,4,7；所以不管前四位取什么数字，个位都有三种情况可以取。

解：这类五位数不含有6的个数为种，则含有6又可以被3整除的五位数的个数为30000-17496=12504种。

点评：此题刚拿到手时感觉无从下手，根据题目意思分析每位含6的个数，比如万位含6，其他位的情况，再考虑千位为6其他位的情况势必得考虑到万位为6的情况，因此，我们可以考虑相反方向，不含6的情况就没有重复这一说了，计算起来要简单的多；其次，如何每种情况都分析到的话，计算量也会相当复杂，比如说万位是1，然后千位是1的时候其他位取什么，千位是2时候其他位取什么，这样计算起来计算量就会相当庞大，因为是被3整除，除数是个一位数，并且除数为3和9时有个特点就是各位数之和能整出3就是3的倍数，各位能整出9就是9的倍数这个特点，可以把前面四位之和看成一个整体，也就是说前四位讨论的情况都可以取，然后再根据和除以3的余数的三种情况进行讨论各位数的取值情况，复杂的题目经过一层层的分析变得简单。

例2.设。

解：假设=0,则原式=1，即=1； （1）

假设，则原式==1,即 （2）

假设，则原式=，即 （3）

（2） （3），得2（）= 1，则=

又因为（1），所以=。

点评：单纯从题目来讲，如果不借助特殊值，是无法分离出来所要求的值，又因为在取1，-1，0的时候多项式可以只用系数表示，所以可以考虑从特殊值入手，求得结果。

随着社会的发展，手机的使用越来越广泛，手机安全问题也相对受到人们的关注，手机也有相应的密码设置，常见的解锁有数字解锁，指纹解锁，人脸识别解锁和安卓手机的九宫格解锁，这里运用组合技术来讨论九宫格解锁的密码个数问题。

例3 (1)从22格子选取2个点，3个点，4个点，进行有序排列,一共就多少种不同情况？

（2）对于九宫格密码的设置，有着这么几个原则：

第一，选择格点至少为四个且每个点只能使用一次；

第二，在同一行或者同一列或者斜着三个点在同一条线上的话，两端的点不可以直接连接，如果中间的点是之前已经用过的，那么这个点就可以被跳过，例如手机九宫格中2到5到3到1是可以的，但是3开始直接到1是不可以的；

第三，点选择好之后连接顺序不同，所产生的情况也是不同。如下图，前两个是直接1到3和1直接到9这两种情况都不满足情况，但是后两种情况，从2出发先到点4，然后从4再到1，之后从1到3这种情况就满足了，因为2之前已经用过了，可以视为不存在了，所以满足情况。

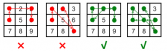
问：安卓手机九宫格的解锁方法一共就多少种？

解（1）我们从两个点开始讨论，四个点取两个点有种，一共是种；取三个点有种，共有种；取四个点的情况只需要考虑排序，即有种。综上共12 24 24=60种情况。

（2）我们首先根据九个点中可以取从4个点一直取到9个点，先讨论取点情况，再根据取点的种类研究出各种情况所有的可能情况，最后得出全部情况的个数。

我们可以根据限制条件得到以下条件，即13、46、79、17、28、39、19、37、31、46、97、71、82、93、91、73这十六种情况存在的条件是在这些数字之前必须前面对应存在2、5、8、4、5、6、5、5、2、5、8、4、5、6、5、5这十六个数字。我们使用组合计数来计算出从4个点取到9个点的情况，如果直接计数的话可能会出现漏数据、重复数据的情况，而且计算量复杂，因此我们可以根据对立面求出不满足条件的情况，然后根据总的情况去掉不满足的情况，得出最终结果。

我们从四个点开始讨论：

从9个点中取4个点，不考虑不满足条件的情况，一共有=3024种，下面我们来找出其中不满足条件的情况。

①上面16种情况放在一二位置，然后后面两个数可以随便选都不满足，如13_ _这种情况，无论后面两个数为什么，都不满足情况，后面两个数取值情况共有种情况，又因为开头的两个数字有16种情况，所以一共有种不满足的情况。

②这16种情况的两个数字放在第二三位置，如_13_和_28_这两种情况，第二三位置取13前面不可以取2、7和9，所以有四种可能性，因为取2的话满足情况，取7和9的话跟①里面的情况冲突，所以第一个位置有四种情况，第四个位置可以任取，有六种可能，所以有46=24种可能，又因为跟13这种情况相同的第二三位置还可以取31、79、97、17、71、39、93、19、91、37、73这十一种情况，一共十二种，所以一共有1224=288种情况；第二三位置取28的情况，第一位不可以取5，其它都可以取，共6种可能，第四位可以取剩下的六种情况，共66=36种，种情况的第二三位置还可以取82、46、64三种情况，一共四种情况，所以共364=144种，所以一共有288 144=432种不满足的情况。

③这16种情况放在第三四位置，如_ _13、_ _28和_ _19，第三四位置取13时候，先考虑第二位不能取2，7和9，共有4种情况，第一位不能取2，所以可以 取剩下的5种情况，但是得考虑前面两位取到①情况的时候，这里第一二位置取46和64时候跟①重复，所以减去，即有45-2=18种，再考虑第二位取7和9的情况，假如第一位是2的话，则在①和②中没有取到不重复，即4713和5913，有两种，所以共18 2=20种，又因为跟13这种情况相同的第二三位置还可以取31、79、97、39、93、37、73这七种情况，一共八种，所以一共有208=160种情况；第三四位置取28的时候第二位置不可以取5，所以可以取6种情况，第一位可以取剩下的5五种情况，又因为第一二位置取值时候不能与①中情况冲突，即不可以取13、31、46、64、79、97、17、71、37、73、39、93、79、97这14种情况，所以共有56-14=16种情况，又因为跟第三四位置取28情况相同的还要82、46和64三种情况，共四种情况，所以一共有164=64种；第三四位为19的情况跟取13情况差不多，唯一不同是2819跟4619这两种情况跟①冲突，故去掉，有18种；又因为与第三位取19的情况相似的还有91、37和73三种，共四种，所以这类情况共184=72种。综上这16种情况放在三四位置不满足的情况共160 64 72=296种。

综上，取四个点时候不满足的情况一共672 432 296=1400种，所以满足条件的情况是3024-1400=1624种不同解锁方式。

根据所给的限制条件以及所要取得的结果，我通过Java代码做了相应的需求分析以及应用，其主要方法是先得出所以排列组合情况数，然后根据条件限制列出不满足条件的所有情况，没得出一种不满足情况的数列，组合情况数就减去一，所取得的结果与组合计数所得结果完全一致，根据从最开始取的四个点推广到五个点以及到九个点（主程序见附录），得出取五个点的时候共7152种不同解锁方式；取六个点的时候有26016种情景；取七个点的时候有72912种情况；取八个点的时候有140704种情况；取九个点的时有140704种情况。综上九宫格解锁的种类共1624 7152 26016 72912 140704 140704=389112种情况。

点评：本题主要是运用了排列组合来解决生活中的安卓手机的九宫格解锁问题，主要方法是组合计数，先列出所有情况，再排除不满足的情况，最终得到我们想要的结果。

4.2 抽屉原理

抽屉原理，也就是我们所熟知的鸽巢原理，是在1934年，著名德国数学家狄利克雷提出的。所谓抽屉原理，简单来说可以形容为假设桌上有十个物品，现在要把这十个物品放在九个抽屉里面，则至少有一个抽屉里面至少放两个物品，应用这一原理可以解决很多涉及存在性的组合问题。

抽屉原理的基本原理:把个物品放在个容器中，，那么至少有一个容器中的物品不少于两个。其表达形式重要有（1）把个物品放在个容器之中，那么必然有一个容器里有或者以上各个数的物品；（2）把个物品分到个容器之中，则必然有一个容器之中物品的个数大于等于个，同时也至少有一个容器中物品的个数小于等于。

通常遇到这类问题如果直接证明不容易说明或者说明力度不够，这又要用到反证法来解决问题，也有些情况需要把所以情况一一列出，下面我们来看几组例题：

例4.一个国际社团的成员来自留个国家共1978个人，用1,2,3…1977，1978来编号。试证明：该社团至少有一个成员的编号或者与他的两个同胞的编号之和相等，或者是其中一个同胞编号的两倍（第20届IMO第六题）^[5]

分析：本题的话如果要直接证明的话，需要把所有情况列举出来，情况复杂，答题繁琐，所以就要考虑运用反证法解决。

证明：要证明本题直接证明复杂度较大，因此我们可以通过用反证法证明与本题相同的下列问题：把数列1,2，…1978按照任意的方式分成六个组，则在这六个组中至少有一个组具有该性质：有一个数等于该组中其它两项的数的和，或者等于其中一个数的二倍。

我们先假设在这六个组中不存在数具备这样的性质，我们把这个性质记做（M）：

我们先来考虑如果有，以及都在同一个组中，那么因为，那么这组数就具备了我们所要证明的性质。

因为，根据抽屉原理，我们可以求出，至少存在一个数组A，其中有大于或者等于330个正整数，我们现在从A中任易取出其中的330个数，最大的数字我们用来表示，我们先用分别减去剩下的329个数，因为这些数全都小于1978并且满足互不相等的条件，根据性质（M），这些差不能够存在于A中，只能出现在其它的五个组当中。又因为，再根据抽屉原理，我们可以求出存在一个数组B，B中存在大于或者等于66个上述的数字，我们可以从B中任易取出66个数字，我们将其中的最大数字用表示，然后再用分别减去数组B中剩下的65个数，这些差既不属于B，同时也不属于A。

我们现在假设其中的某个数属于A，因为和分别可以写成,,其中的都是属于A，于是有。这就与A具备的性质（M）违背，这就说明上述65个数必然存在属于其它五个数组的。

因为，根据抽屉原理，则存在一个组C，至少会具有上述65个整数中的17…我们可以根据这一推理思想，最后能够得到一个数组F，在F中至少会存在两个数字，用大数减去小数是一个小于1978的自然数，可是它不在A,B,C,D,E,F中的任何一个组总，这就是一个矛盾，矛盾说明至少有一个组不具备性质（M），这也就说明本题的论证是正确的。

点评：本题是从 一个大的数据入手，但通过构造抽屉，层层减小范围，最终从小的方面回推到最开始的问题，从大化小，以小解大。

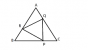
例5.设ABC为一个等边三角形，E是三边上点的全体。对于每一个把E分成两个不相交子集的分划，问这两个子集中是否至少有一个子集包含着一个直角三角形的三个顶点.（第24届IMO第四题）^[5]

证明： 如上边图所示，我们先在AB,BC,CA的边上分别取R,P,Q三个点,这些点的选取满足

BR=。

我们可以明显的看出，△ARQ，△BPR和△CQR都是直角三角形。并且它们的两个锐角都分别是和。我们假设的两个非空子集，同时满足和。根据抽屉原理，我们可以得出在P,Q,R中，至少存在两个点是属于一个子集的。假设P,Q,我们如果能在BC上找到除了P点之外的点属于，本题即得证。

我们先假设在BC上，除了P点之外的所有点都属于，那么只要在AB上能够找到除B点之外的S点满足 ，设S为S在BC上的投影点，则△SSB即为直角三角形。再假设AB内的每一个点都不属于，这也就意味着除了B之外的点都属于，则R,A都属于，因此可以推出A,Q,R属于，并且三角形AQR为直角三角形，从而此题得证。

点评：本题是根据分割图形来构造抽屉原理，在图形中根据已知条件和要求证的问题，做世道的分割分类，然后进行讨论，最终得到我们想要的结果。

4.3 容斥原理

定义：在计数时，我们要做到既不能重复计数，也不能出现遗漏。为了避免不同部分之间重合的数据被重复计数，一些人就尝试着研究出来了全新的计数方法，其主要思想是先不考虑重复的部分，将各个部分的数量进行计数，然后再考虑重复的部分，再次去掉，这样做就保证了计数到最后既不会出现重复数据也不会出现遗漏的情况，我们把这种计数方法叫做容斥原理。

谈到容斥原理，我们要从德摩根定理说起：若A和B是集合U的子集，则有

（1）

（2）

容斥原理的基本公式：

下面我们通过例题来展现容斥原理的应用：

例6.设与是正整数，其中, 平面上有个点，其中任意三个点不共线。如果其中每个点都至少有和其它个点用线段连结，则连结的线段中至少有三条围城一个三角形。（波兰1968年数学竞赛，第五题）^[6]

证明：因为，，所以可以得出，这表明：在这个点中存在和，这两点连成了一个线段，剩下的点构成了集合，我们记做集合X，X中的所有点与连接的线段的集合记做A，这个面与连结的所有点的集合记做B，显然是X的子集，因此有.另一方面，由已知条件，,则根据容斥原理，有

,

即

，

这也就证明了，也就是说中必然有一个点，它与构成一个三角形

点评：本题根据点和与其它点相连的线为容器，探求两容器之间是否有交集，若有，则三条线构成一个三角形，这是一道典型的容斥原理题，本题需要根据数据之间的关系证明两个交集不为0，即证明有三条围城一个三角形。

例7.由数字1,2,和3组成的位数，要求n位数中的1,2和3的每一个至少出现一次，求所有这样位数的个数。（匈牙利奥林匹克1998年第八题）^[6]

解：我们首先将由数字为1,2,和3组成的位数构成的集合记做，则

假设S中所有不含的位数的集合记做(=1,2,3),则是S中所有含有数字的位数的集合即是S中同时含有数字1,2和3的位数的全体构成的集合。由逐步淘汰原理，

因为( )是S中所有不含数字的位数的集合，所以

，

我们令和的位数的集合，所以

，

根据题意显然有，则

，

所以根据题目要求可以得出位数的个数为

。

点评：此题需要证明1,2,3至少出现一次的数目，那么我们需要考虑对立面，即不出现1或者不出现2或者不出现3的次数，在考虑这些的同时，我们还要考虑到重复出现情况的次数，即同时不出现1和2或者同时不出现1和3和同时不出现2和3的次数会计算两次，需要减去，同时不出现1和2和3的理论上被减去两次，所以最后需要再加上一次，然后运用容器原理构造容器，得出结果。

4.4 递推关系

组合数学中最重要内容就是计数，许多计数问题因为过去复杂，需要化为递推关系来求解，计算机中的算法也是应用了递推关系。

定义：如果数列{}的前项与它的前一项或者几项的关系可以用一个式子表示，这就是递推关系。

设是个常数，且,则递推关系

称为阶常系数线性齐次递推关系。

剩余内容已隐藏，请支付后下载全文，论文总字数：15424字