Lagrange 乘数法的推广及应用

论文总字数：9493字

目 录

1前言 3

2 Lagrange乘数法 3

2.1 Lagrange乘数法的定义及基本步骤 3

2.2 Lagrange乘数法的几何意义 4

2.3 Lagrange乘数法的向量证明 5

3 Lagrange乘数法的部分推广 7

3.1 多元函数最值、极值求解问题 7

3.2 Lagrange乘数法在多元对称函数最值求解的运用 9

3.3 Lagrange乘数法在不等式证明中的运用 11

4 Lagrange乘数法的应用 13

4.1 Lagrange乘数法在串并联电路中的应用 13

4.2 Lagrange乘数法在融合滤波中的相关应用 15

4.3 Lagrange在工程学中的应用 17

5结论 17

参考文献 18

致谢 19

Lagrange乘数法的推广及应用

钱天麒

，China

Abstract：In this paper ,we first give the definition of the Lagrange multiplier method and the basic problem-solving steps, then we explain its geometrical meaning and prove the Lagrange multiplier method by the vector form. Secondly, by using the Lagrange multiplier method,we get the maximum and extreme values of simple multivariable function and multivariate symmetry function,and then give the inequality proof. Finally,we dicuss some applications of the Lagrange multiplier method in fusion filtering, electrical and other physical fields .

Key words：Lagrange multiplier method; Maximum values; Inequality; Fusion filtering

1前言

Lagrange乘数法(以露易斯·拉格朗日命名)是一种在多限制条件下寻找目标多元函数驻点的一种有效方法。其把个变量与个限制条件转化为个变量的方程组,然后进行求解获得其可能极值点。这种方法引入了一组新的未知量——Lagrange乘数,其表现为约束方程梯度构成的线性组合系数。

Lagrange乘数法虽然古老,但依旧在被不停的研究与拓展。在文献[1]、[2]中，王凯阳与曹淑芳比较详细地介绍了Lagrange乘数法各参数的意义以及一些基本的性质，并给出了相应的例子。而乔建赋在文献[3]中，利用向量形式给出了Lagrange乘数法在二位、三维乃至维的证明方法。

在Lagrange乘数法的运用及推广中，最容易想到的就是多元函数极值、最值的求解问题。例如：在文献[4]中，马统一先是利用Lagrange乘数法证明了目标多元对称函数驻点的一个必要条件(即元对称函数的驻点其中有个变量相等)，之后又利用导数及其相关性质给出了驻点满足其最值的证明，本文也将对[4]中的多元对称函数变式给出相似的解法。另外，把Lagrange乘数法运用到不等式的证明中，我们可以得到一种不同于传统方法的简易证明方法。如在文献[5]、[6]中，雒秋明和陈红蕊利用Lagrange乘数法对基本不等式、赫尔德不等式等不等式进行了更为简洁明了的证明。

Lagrange乘数法在相关物理领域、工程学领域也有广泛应用：如在[8]中，邵建新利用Lagrange乘数法研究了在并联电路中电阻的耗散问题，分析了在串联电路中电容的储能问题，考虑了带电球体的电荷分布问题。而在[9]中，孟赵玲考虑了带两传感器的一维离散随机线性系统，然后利用Lagrange乘数法求出该系统达到滤波要求的相关系数。另外,罗笑南在文献[10]中通过Lagrange乘数法，对机翼载荷、可靠性分析和工程学模型进行了计算研究。

本文在上述文献的基础上，首先对Lagrange乘数法的定义与意义给出了简单的叙述，同时利用向量形式对Lagrange乘数法进行了证明；其次介绍了Lagrange乘数法在多元函数极值最值问题上的运用，给出了利用Lagrange乘数法进行不等式证明的思想与证明步骤；最后在物理和工程学的相关领域，应用Lagrange乘数法计算分析相关问题。

2 Lagrange乘数法

下面我们先简单介绍Lagrange乘数法的基础知识。

2.1 Lagrange乘数法的定义及基本步骤

定义2.1.1：给定n元函数 以及约束条件

为了求得z在给定条件下的极值，先作Lagrange函数：

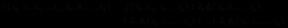
然后对L的各个分量求偏导并使其为零，就得到如下的方程组：

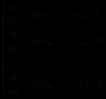
一共个变量以及个方程。我们解得函数的驻点为，然后利

用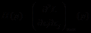判断解的性质。若正定，则为极小值点；若为负定，则为极大值点；若不定，则需要根据条件做进一步判断。

其中关键参数的意义：是约束条件组对目标函数极值点位置影响的度量；或者说表示了极值点位置随约束条件变化而变化的“灵敏度”。限制条件改变时，对应目标函数的最优值也将随之产生变化。经济学上，参数常称为“边际效益”，其表示为资源对最大利益的影响程度。

2.2 Lagrange乘数法的几何意义

接下来将用一个三维的例子来说明Lagrange乘数法的几何意义。

几何意义：在局部极值点上，目标函数所表出曲面的梯度向量和约束条件表出曲面的梯度向量是共线的，而Lagrange乘数代表的就是这两个共线梯度向量的比例。

给定三元函数以及约束条件：

如图，曲面为约束条件，而(图中的表示的是不同值情况下，的图像)为目标函数。设偏导存在且连续，我们可以看到在条件下的可能极值点必为右图中曲面与相切的点，记为(该点可能不止一个,这里只对其中的一个点为例，同时要注意相切的点也不一定为原函数的极值点)。

从而有公共法线，故两条曲线在点处的法向量平行。

即有：

剩余内容已隐藏，请支付后下载全文，论文总字数：9493字