论文总字数:4744字
目 录
1.引言 5
2.光滑函数的Sobolev不等式 5
3.有界变差函数的Sobolev不等式 7
4.经典微分几何证明 11
5.参考文献 12
6.致谢 13
从Sobolev不等式到等周不等式
蒋术谙
, China
Abstract : In this article,we introduce Sobolev inequalities with proofs and apply them to show isoperimetric inequalities. First, we present the proof of Sobolev inequality for smooth functions,and then generalize it to the space of functions of bounded variations. Based on this ,we prove isoperimetric inequalities for Caccioppoli sets,and make comparison with the classical geometric proof.
Keywords: Sobolev inequality,isoperimetric inequality,Caccioppoli set
1.引言
等周不等式是经典的几何不等式。古希腊人就已经知道当平面图形的周长固定时,圆的面积是最大的。但其严格证明一直到近代才利用微分几何工具给出。
Sobolev空间和Sobolev不等式始自于前苏联数学家Sobolev,伴随着变分法、偏微分方程理论发展起来。 以Sobolev不等式为代表的一大类泛函不等式已经成为许多领域的基本工具。
在Sobolev空间理论发展早期,Maz`ya等人就注意到了Sobolev不等式与等周不等式之间的联系。本文基于这一想法,并利用有界变差函数和Caccioppoli集的概念,将Sobolev不等式推广到有界变差函数上,进而证明等周不等式。
本文第二章介绍了光滑函数的Sobolev不等式,第三章讨论了有界变差函数的Sobolev不等式, 并证明了等周不等式。作为对比,第四章介绍了等周不等式的经典微分几何证明。
- 光滑函数的Sobolev不等式
首先,在介绍Sobolev不等式之前,我们需要定义Sobolev空间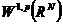 。
。
定义2.1: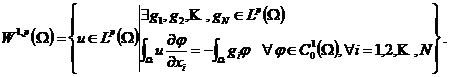
此处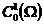 指
指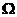 上一阶连续可微的紧支撑函数全体。
上一阶连续可微的紧支撑函数全体。
对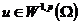 ,定义弱导数
,定义弱导数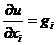 ,我们有
,我们有
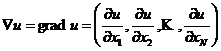 .
.
Sobolev空间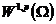 可以赋予如下的范数构成一个Banach空间:
可以赋予如下的范数构成一个Banach空间:
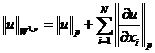 .
.
本节的主要结果是下面的Sobolev不等式。
定理2.1(Sobolev不等式):令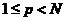 ,则
,则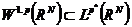 ,其中
,其中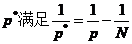 ,并且存在一个常数
,并且存在一个常数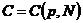 ,使得
,使得
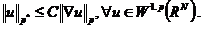
在证明Sobolev不等式时,我们需要用到如下一个事实: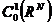 在
在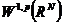 中稠密。
中稠密。
证明:我们引入一个引理,令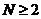 并且令
并且令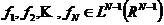 。对
。对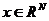 和
和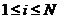 建立
建立
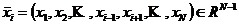 .
.
即,从列表中省略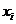 。函数
。函数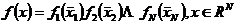 属于
属于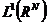 并且
并且
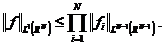
我们先讨论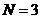 的情况。
的情况。
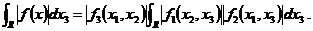
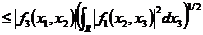 (Cauchy–Schwarz不等式)。
(Cauchy–Schwarz不等式)。
再次运用Cauchy-Schwarz不等式得到
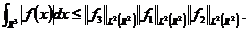
通过归纳法得到一般情况,假设结论对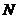 成立,然后考虑
成立,然后考虑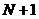 维的情形。
维的情形。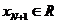 ; 根据赫尔德不等式,
; 根据赫尔德不等式,
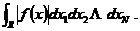
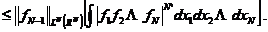
(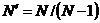 )将归纳假设应用于函数
)将归纳假设应用于函数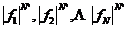 ,我们得到
,我们得到
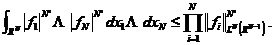
从中得出结论
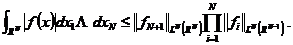
现在变化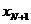 ,函数
,函数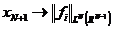 中的每一个都属于
中的每一个都属于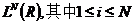 。假设
。假设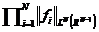 属于
属于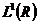 ,
,
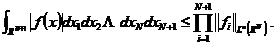
这里我们仅考虑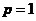 的情况。当
的情况。当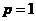 并且
并且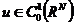 时
时
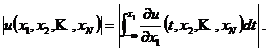
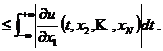
相似的,对于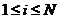
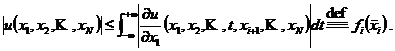
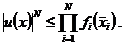
我们从引理可以推出
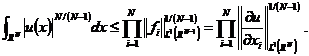
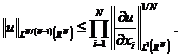
所以当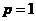 并且
并且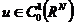 时,我们得到了Sobolev不等式的证明。一般情形可通过稠密性得到。
时,我们得到了Sobolev不等式的证明。一般情形可通过稠密性得到。
3.有界变差函数的Sobolev不等式
利用检验函数的想法,我们定义一个函数的全变差。
定义3.1:假设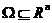 是一个开集并且
是一个开集并且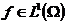 ,定义
,定义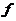 的全变差
的全变差
剩余内容已隐藏,请支付后下载全文,论文总字数:4744字


