一类含时滞的SEIR传染病模型的性质分析

论文总字数：8078字

目 录

1 研究背景及现状 3

2 模型的建立 4

3 基本定义及引理 6

4 理论准备 7

5 全局稳定性 9

6 局部稳定性 12

7 持久性 13

8 结论 14

参考文献： 15

致谢 16

一类含时滞的SEIR传染病模型的性质分析

葛鑫

，China

Abstract：In this paper,we study some properties of a kind of SEIR epidemic model,and the time-delay effect of infected person on susceptible person is considered. Firstly,the positivity of

the solution for epidemical model are studied.On the basis, it decides the stability of the disease, the existence and destruction when the basic reproductive number satisfies certain conditions. The disease-free equilibrium is globally asymptotically stable by constructing Lyapunov functional when the basic reproductive number .The disease will be eliminated. Furthermore when ,the positive equilibrium that is locally asymptotically stable and permanent is proved.At this time it will continue to form endemic disease. At the same time, the local stability of the equilibrium is studied through characteristic equation.These conclusions provide some theoretical basis for controlling the spread of disease.

Key words：epidemic model;global stability;the basic reproduction number;equilibrium point.

1. 研究背景及现状

传染病是因多种病毒、细菌导致个体和个体或群体和群体之间相互传播的一类疾病．在历史上，传染病的每次爆发都能使人类的生存和发展受到巨大的损失，如令人印象深刻的天花和流感等，每当这些疾病泛滥成灾都夺去了成千上万的生命．虽然一部分疾病已经能够有效的预防和治疗，但是近年来由于SARS和甲型H1N1等病毒的传播，给人们的生命安全带来极大的危害，使人们更加强化了对传染病的预防和控制意识．传染病的流行关系到人类的生存，也会对人类的生活质量和工作效率产生影响，是不可忽视的．因此，我们需要用一些数学模型来讨论关于传染病的一些问题，用理论方法找到控制疾病蔓延的措施．

 1760年，传染病动力学模型是DanielBernoulli在研究如何有效预防天花时得到．直到1927年，Earmark和 Mekendrick提出了非常经典的SIR仓室模型.紧接着，到了1932年他们再次建立了SIS模型，并在此基础上，得到区别传染病是否将会继续流行的经典结论——“阈值理论”，为后来传染病模型的发展奠定了基础．随着不断的研究，人们又陆续引入其它因素，提出了SIRS，SIRES等模型．

学者们早期研究的传染病模型基本上都假定研究对象的总数为常数，然而这个假定是有局限性的，只有在较短时间、隔离环境、出生率与死亡率能够平衡、由于其它疾病死亡的比率可以忽略时成立.而近些年研究的模型相比前者而言比较符合实际，考虑的问题也更加全面，因研究的方向不同可分为三类：模型包含的因素增多，例如时间长短、年龄分布、是否接触、物种流动等；模型维数不断增加，此时可以研究传染病于若干种群之间传染与扩散问题；结合某些具体的疾病类型或案例进行细致深入地分析和研究，这种方法可以较为细致的分析某种传染病的相关性质，及时有效的找出应对方案.因为研究的系统更加贴近实际生活，因此模型的建立变得复杂化、多样化，理论研究也将不断遇到各种困难.[1]中介绍了几种分析传染病模型方法和理论．

1. 模型的建立

传染病动力学在传染病进行定性分析中有着重要地位，通过建立数学模型来分析疾病的感染和扩散机制，预测传染病未来的流行趋势，从而为疾病的预防、控制和治疗提供理论依据．由于疾病的类型不同，疾病传播过程的规律、特点和复杂程度也自然不同，而且还会受到各种因素的影响．传染病研究有很多方法，其中本文运用比较经典的仓室模型．通过种群个体在疾病传播中的表现形式和特征，可将种群分为几个仓室，进一步得到具体的数学模型．为了便于研究，我们仅讨论关键因素并作出合理假设．例如，双线性感染率为时，有如下SEIR模型

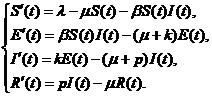(1)

这里分别表示在t时刻易感者、潜伏者、染病者、恢复者的数量．各个形态在疾病传播过程中相互转化，且不会同时属于多个类型．种群总量为．表示种群的输入率，即无病时整个群体维持平衡态时的数量．为自然死亡率．为潜伏者对疾病的自身免疫和恢复能力．表示潜伏者转化为染病者的比率，则表示潜伏期[2]．

传染病的接触率，即单位时间内无病种群转化为患病者的数量，这是影响传染病模型的一个重要因素．接触率的一般形式如下

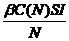
其中．表示无病类型和患病类型的有效接触率是关于种群总量N的函数，但不可能随着N的增长而无限制的增长，这显然与实际情况不符．因此，根据疾病在传播过程中对易感者或染病者的饱和反应[3]，分别得到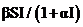和．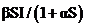

潜伏者和染病者均为患病种群，对于系统，我们可以理解为易感者一旦接触染病者将瞬间变成潜伏者．然而，在现实应用中，疾病的传染不是短时间内实现的，即易感者接触染病者成为潜伏者总会存在时间滞后．对此，得到如下具有时滞，接触率为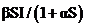的SEIR模型

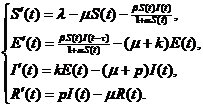(2)

这里表示时间滞后，即易感者与染病者接触变成潜伏者并不是瞬时的，而是需要一段时间．对于接触率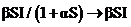，当易感者S的个数较少时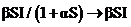，，此时因易感者和感染者接触，导致潜伏人数呈线性增长；当S数量较大，时，非线性接触率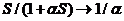，即当易感种群的规模远远超过染病者时，潜伏者的数量不会无限增加，而是趋于一个饱和数．因此，与模型中的双线性型传染率相比，上述传染率比较有实际意义且更加合理．

构造一个Banach空间，用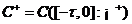表示的赋上确界的连续泛函，由于模型的生物意义，则可得到系统的初始条件如下

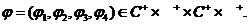(3)

再根据泛函微分方程理论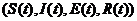，为系统(2)在上述初始条件下仅有的解，可以得到以下结论：

引理 模型(2)在上述初始条件(3)的解非负并且在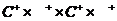内一致有界．

证明　首先证明非负性．对于系统(2)的第一个方程，当时，可得，即．对于系统(2)的其他三个方程，有

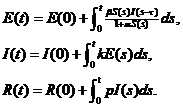
因此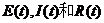非负，即证得系统(2)的解非负．

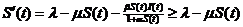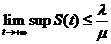继续考虑模型(2)的第一个方程，，则．令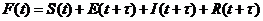．由解的非负性，有

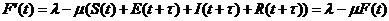
则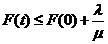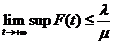，．根据的定义，系统(2)的解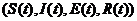一致有界．

从之前的证明我们可以知道系统(2)的动力学可以在可行域

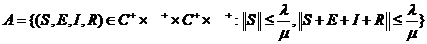
上进行分析．

1. 基本定义及引理

定义3.1（基本再生数）

传染病学中，发病初期，某个群体趋于较为稳定的平衡态且所有个体全都是易感者，一个染病者经过一段时间后，在单位患病内所传染的人数，可以称为基本再生数．

剩余内容已隐藏，请支付后下载全文，论文总字数：8078字