论文总字数:7835字
目 录
1.引言 5
2. 变量替换法 6
3. 待定函数法(常数变易法) 8
4. 幂级数解法 10
5.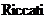 方程解法 12
方程解法 12
6.参考文献 14
7.致谢 16
二阶变系数线性微分方程的几种解法
张晋源
,China
Abstract:In mathematical theory,the ordinary differential equation is an important part to be researched.With the large number of relevant books and papers published,the methods for solving solution to ordinary differential equations have got more and more developments.Nowadays,the most used method for solving solution to second order linear differential equation with variable coefficients is of power-series,However,it requires a lot of conditions and could not give analytical solutions,which causes many problems in theory.Therefore,searching for general solutions for second order linear differential equation with variable coefficients is very important in all theories of differential equation.In this paper,there will be four solutions to be introduced,which are recently most used to solve some special second order linear differential equation with variable coefficients.After that the readers can have more information about this kind of equations.
Key words:Second Order Linear Differential Equation with Variable Coefficients;Variable Substitution;Undetermined Function;Riccati Equation;Power Series.
1.引言
对微分方程系统性求解的要求是由社会生产所提出的,因为微分方程是自然规律的反映,它既能给某些已有现象一个客观的解释,同时也能根据已有现象对可能出现的新现象进行预测.可以说微分方程是研究自然和社会科学中客观对象转化和变化规律最为直接的手段.随着微分方程的不断发展,越来越多的领域都或多或少的运用了其相关知识,即物理学,医药学,计算机应用,机床数控等等.而在线性微分方程领域,低阶常系数线性微分方程及其求解尤为重要,我们已经知道,所有非齐次线性微分方程的求解过程都能够转化成对相关齐次线性微分方程基本解的求解过程,与此同时,也可以使用降阶法把高阶方程的求解转换成对低阶(一阶,二阶)方程的求解.但是到目前为止,对于二阶变系数线性微分方程还没有通用的解决手段,所以本文具有一定的理论研究价值.
虽然二阶变系数线性微分方程应用广泛,求解结构理论上来说也算比较完善,但对于一般线性微分方程的求解问题,至今还没能找到更为一般的方法.除了已知的某些特殊的函数方程有固定解法,很多方程也只能利用幂级数解法来解决.我们不妨来看看以下的二阶变系数齐次线性微分方程:
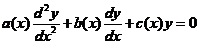
通常情况下我们要先确定系数函数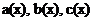 有无公因子
有无公因子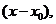 有则削去,考虑原方程的同解方程,如果没有则分两种情况来考虑方程初值问题解的存在唯一性问题.也就是要确定原方程的常点,借助常点来求一个形式幂级数解,在分别求出它的一阶和二阶导数之后,再回代,逐一比较x的同次幂的系数,再用比值判别法判断形式幂级数的敛散性,从而求出原方程的通解.这就是我前面所说的幂级数解法,显然该方法计算量大,步骤繁多,并且由这种方法得到的通解是以无穷级数形式所给出的,这就不利于对方程做进一步的研究.因此,寻求一种简单可行的计算方法是非常紧要且必要的.
有则削去,考虑原方程的同解方程,如果没有则分两种情况来考虑方程初值问题解的存在唯一性问题.也就是要确定原方程的常点,借助常点来求一个形式幂级数解,在分别求出它的一阶和二阶导数之后,再回代,逐一比较x的同次幂的系数,再用比值判别法判断形式幂级数的敛散性,从而求出原方程的通解.这就是我前面所说的幂级数解法,显然该方法计算量大,步骤繁多,并且由这种方法得到的通解是以无穷级数形式所给出的,这就不利于对方程做进一步的研究.因此,寻求一种简单可行的计算方法是非常紧要且必要的.
国内外很多学者已经研究出,可利用一些特殊变换,把变系数方程转化为常系数方程来求解,比如众所周知的Euler方程.然而这些方法都是借用一些特定变换来求解一些特定微分方程,局限性很大,不利于全面的深入研究.在当代,尽管我们可以借助计算机软件来求解方程,但是相关计算机软件在理论上还不是很完善,缺乏智能判断,不能真正解决问题,有时候甚至会使问题变得更加复杂化.
鉴于人们在微分方程领域所遇到的种种问题,尤其是对于二阶变系数线性微分方程一般性解法的研究问题,以及国内外相关理论研究发展现状,本人写下了这篇文章,希望能与大家共同探讨这一问题.我在钻研前人研究成果的基础上,配合自己的独立思考,总结出了四种最有价值的特殊解法,现将其介绍给大家,让不了解该内容的人能对此有一定的了解,并希望熟知此内容的人能提出宝贵的建议和意见.
2. 变量替换法
对于某二阶变系数齐次线性微分方程,如果已经知道它的一个不是零的解,我们就可以求得其通解,对于同等非齐次的微分方程,我们将在稍后进行说明:
首先,我们考虑一个变系数二阶齐次线性方程
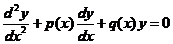
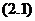
设它已知不是零的解为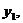 对他进行变量的替换
对他进行变量的替换
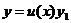
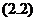
其中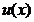 是未知函数,对
是未知函数,对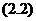 求导得
求导得
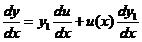
再求二阶导数有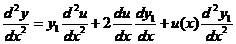
把它代入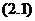 式得
式得
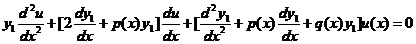
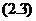
这是关于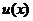 的一个变系数二阶齐次线性方程,所有系数为
的一个变系数二阶齐次线性方程,所有系数为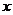 已知函数,因为
已知函数,因为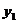 是方程
是方程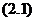 一个解,所以恒有
一个解,所以恒有
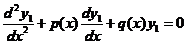
所以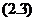 式可化为
式可化为
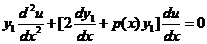
再作变量替换,令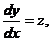 得
得
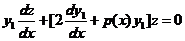
分离变量得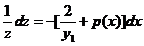
两边求积分,得到通解
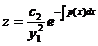
其中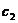 为任意常数.
为任意常数.
再积分得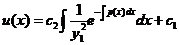 ,将其回代得到方程
,将其回代得到方程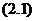 的通解
的通解
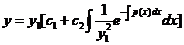
这就是我们所熟知的刘维尔公式.
说明:上面所说二次变换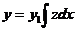 并不影响微分方程右端,所以对于已知变系数二阶非齐次线性方程,假如已知其对应齐次方程的某不是零的解,我们也能通过这种变换来达到降阶的目的,从而求得方程的解.
并不影响微分方程右端,所以对于已知变系数二阶非齐次线性方程,假如已知其对应齐次方程的某不是零的解,我们也能通过这种变换来达到降阶的目的,从而求得方程的解.
例1 已知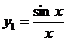 是
是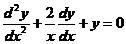 非零解,求出此微分方程通解.
非零解,求出此微分方程通解.
剩余内容已隐藏,请支付后下载全文,论文总字数:7835字


