论文总字数:11107字
目 录
0、引言 3
1、问题的提出 3
2、多元函数取极值的判别方法 3
2.1二元函数的极值的定理式 3
2.2多元函数极值的判别方法 4
3、简单的不等式证明 4
3.1求有约束条件类的不等式 5
3.2拉格朗日乘数法求解几何类不等式的问题 6
3.3求证常见的不等式的几道例题 8
4、几个重要的不等式证明 9
5、拉格朗日乘数法的延伸 16
6、结论 17
7、讨论 18
参考文献 19
致谢 20
拉格朗日乘数法及其在不等式证明中的应用
陈丽媛
,China
Abstract: The method of Lagrange multiplier is a center in this paper, which has also application in the proof of inequality.First of all, the article regards the Lagrange multiplier method as the principal line. Based on the extremum of binary function, where necessary condition and sufficient condition are deeply discussed, we extended related theory to multivariate functions.Then it is applied into the proof of inequality.For individual examples, several kinds of mathematical methods are compared with the Lagrange multiplier method to comprehend advantages and disadvantages.Then we focus on the application to several classic inequalities. Eventually, the Lagrange multiplier methods are extended.At the end of this article, we summarize the procedural points and the skills about the practical significance and maneuverability in the application of the method.This way can be used widely in various fields, in order to solve further trouble in the future.
Key words: extremum; Lagrange multiplier method; inequality; application
0、引言
拉格朗日乘数法是高等数学课程中的用于求解条件极值等最优问题的经典法则,我们通过对条件极值问题求解步骤和解题技巧的了解,可以应用于不等式证明.通过这样的解题思路,将其运用到不等式证明中去,对于处理实际问题具有着里程碑的意义.在我们所学的数学分析中,其中拉格朗日乘数法在极值类问题中有着举足轻重的地位,然而,却拉格朗日乘数法撰写的并不是很深入,也没有举出更多的例子,往往都是一笔带过.本文就对该法进行基础理解后,并在证明不等式的过程中加以活用,发现随着条件的设置的不同,该法的运用在优化不等式问题的基础上,更有意想不到的结果,并与其它数学方法再加以对照,总结其优劣势.下面,我们就拉格朗日乘数法的运用展开叙述的篇章.
1、问题的提出
不等式的解题方法一向是数学学术界长久研究的重点课题.对于不等式的证明方法种类纷繁复杂,并且对于不等式证明的技巧灵活多变,因此,使得在解决不等式问题上变得束手束脚,难以在大体上得到好方法的掌握.基于这个问题,对于数学分析中的多元函数条件极值理论中,提及的拉格朗日乘数法,但由于该篇幅较少,教材中往往一笔带过,并没有详细论述.通过对于拉格朗日乘数法的深入研究,发现该法也可以解决不等式类的题目,并且相比其他更具有技巧性的方法而言,该法显得更直接、更易掌握且更具程序性的方法.本论文以拉格朗日乘数法融入到不等式运用中,解决该类相关问题,对于往后该法运用于实际研究会有着积极且重大的意义.
2、多元函数取极值的判别方法
详读文献[1]至文献[5],对于多元函数的定义和相关定理有基础性的了解.接着,就二元函数在取极值的必要条件和充分条件做更加详细的探讨.然后,延伸到多元函数中,深刻地领悟取极值的判定.
2.1二元函数的极值的定理
多元函数在极值中有着较为普遍且重要的应用,我们就二元函数进行简单了解一下求解极值的必要条件和充分条件.
定理1[3](必要条件) 设函数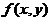 在点
在点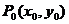 处达到极值,并且存在
处达到极值,并且存在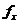 、
、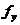 ,则
,则
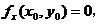
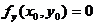 .
.
定理2[3](充分条件) 设点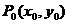 是二元函数
是二元函数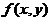 的一个驻点,且二元函数在
的一个驻点,且二元函数在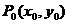 的某个领域内具有二阶连续偏导数,则当海赛矩阵为正定,即
的某个领域内具有二阶连续偏导数,则当海赛矩阵为正定,即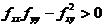 ,
,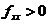 ,则函数在点
,则函数在点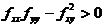 处取得极小值;当海赛矩阵为负定,即
处取得极小值;当海赛矩阵为负定,即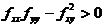 ,
,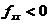 ,则函数在点
,则函数在点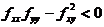 处取得极大值;当海赛矩阵为不定,即
处取得极大值;当海赛矩阵为不定,即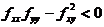 ,则函数在点
,则函数在点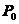 处不取极值.
处不取极值.
注1 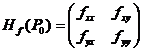 ,称为
,称为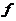 在点
在点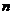 的二元函数的海赛矩阵.
的二元函数的海赛矩阵.
2.2多元函数极值的判别方法
通过2.1的定理复述,初步认识了二元函数取极值的条件.然而,在拉格朗日乘数法的运用中,往往仅获得必要条件.因此,我们从文献[3]中掌握二元函数极值定理以及相关定理证明后,就必要条件,通过按照严格的数学理论和实际意义,接下来深入探讨多元函数取极值的必要条件的判别方法.
定理3[6] 设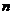 元函数
元函数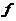 在点
在点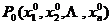 的某领域
的某领域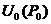 内有二阶连续偏导,且
内有二阶连续偏导,且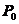 是
是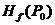 的稳定点,则
的稳定点,则
- 当
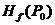 是正定时,
是正定时,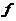 在
在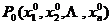 取得极小值;
取得极小值; - 当
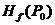 是负定时,
是负定时,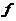 在
在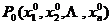 取得极大值;
取得极大值; - 当
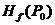 是不定时,
是不定时,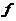 在
在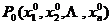 不能取得极值.
不能取得极值.
其中,
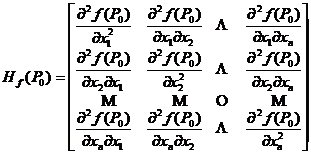 .
.
剩余内容已隐藏,请支付后下载全文,论文总字数:11107字


