论文总字数：14161字

目 录

一 引言 1

二 图论和数学竞赛的介绍 1

2.1图论的介绍 1

2.2数学竞赛的介绍 1

三 数学竞赛中的图论问题 2

3.1欧拉问题在数学竞赛中的应用 2

3.2汉密尔顿圈在数学竞赛中的应用： 3

3.3匹配问题在数学竞赛中的应用 4

3.4着色问题在数学竞赛中的应用 6

3.4.1棋盘染色问题 6

3.4.2几何染色问题 7

3.4.3地图染色问题 8

3.4.4五色定理的证明 9

3.4.5四色定理的实现 10

四 总结 12

参考文献 13

五 致谢 13

附录 14

一 引言

当今社会，日新月茂，越来越多的情况需要使用到离散的数学模型，而图论作为离散的一个分支，其也得到了蓬勃的发展，图论受到了更多人的广泛关注。

由于图论在物理，化学，生物，计算机等发多面都有运用，所以图论自然而然的成为了数学竞赛中不可或缺的一种题型，每年各种类型的数学竞赛或多或少会出现一些图论的题目，比如1989年第三十届国际数学竞赛二试中就有一条图论的题目，之后十八届美国数学竞赛中同样出现了图论题目，这些正印证了图论正与数学竞赛建立了广泛的联系。

本文将涉及到图论问题中的欧拉回路问题，汉密尔顿回路问题，着色问题等，而这些题目都来源自数学竞赛，我将对这些题目做一些分析，总结出解决这类问题需要掌握的技能和一些技巧。

本文在结合染色问题的基础上，会对地图染色问题做一些拓展，通过编程的方式实现四色定理，并归纳地图染色的不同情形。

二 图论和数学竞赛的介绍

2.1图论的介绍

图论，从字面上讲，就是关于图的理论，然而，这里的图，并非几何里的几何图形，也不是美术上的图画，而是在一个平面上有很多点，我们用直线把它们连接起来，成为边而构成的一个平面图,记作。

在有些图中，它的一些边的2个端点互相重合，它们连接成一个圆圈，我们称之为环，既没有环有不存在重复边的图叫做简单图，相应的，存在环或者重复边的图就称为复杂图，不连边的顶点叫做孤立点。

随机选取中的一个顶点,所有以为一个端点的边的数量叫做顶点的度，记作，又称。

如果对于简单图，它的顶点集合划分成的两个子集和（注意：的顶点不能与的顶点相邻）中所有边的端点都分别在这2个子集中，那么图就被称为二部分图。

当然，图论也被当做是一种生活中的数学，它在物理学，化学，计算机技术，运筹学等领域都有广泛的使用。

2.2数学竞赛的介绍

数学竞赛本质上是一种智力竞赛，它起源于苏联。自1894年匈牙利第一次正式举办数学竞赛以来，其已经成功举办过90多届数学竞赛，匈牙利可以说是数学竞赛的发源地，而我国自1956年以来，同样也成功举办了很多次数学竞赛，无论是小学生，初中生，高中生还是大学生，参加数学竞赛都成了一种惯例。

伴随着数学竞赛的火热，竞赛数学也随之产生，这门新兴的课程通过研究数学竞赛的题目，提出了许多新的解题思想和解题技巧，丰富了数学课外教育，同时数学竞赛中出现的一些数论，代数，几何，组合数学的题目，我们在学习了以后，数学能力也会有质的飞越。

图论作为组合数学的一个分支，同样在数学竞赛题中占有一定的比重，这类问题对于数学竞赛有着深刻的意义，它考察了我们的空间想象能力，作图能力等多方面的能力，是数学竞赛不可或缺的一部分。而通过数学竞赛，图论的研究也得到了推广，两者相互促进，相辅相成。

三 数学竞赛中的图论问题

3.1欧拉问题在数学竞赛中的应用

提及欧拉回路问题，首先要引申到著名的七桥问题，据说哥尼斯堡有一条河，河中有一个岛，共建七座桥联系被河隔开的四块陆地,当时，这个城里的人希望能做一次散步。从一点出发，能恰好经过每个桥一次，最后再回到原点。

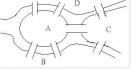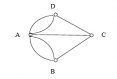图（1）图（2）

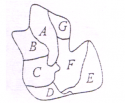
这个问题已经被欧拉证明了，是不可能成立的，他把图中分开的陆地称之为A,B,C,D,7座桥为连接这些陆地的线（见图（1））。

那么这个问题就由实际问题转换成了一个简单的几何图形（见图（2）），即一条一笔画的问题，因为该图并不能一笔画成，所以原假想是不成立的。

七桥问题揭开了图论研究的新篇章，所以我们将这个问题视为图论研究的鼻祖。

欧拉回路和欧拉路径的概念：如果一条线路，它恰好经过每条边一次且不重复，那么这条路径称为欧拉路径，如果这条路径恰好还是一个圈，则为欧拉回路。

具有欧拉回路的图称为欧拉图。我们可以通过下面的判定方式来判断欧拉回路和路径是否存在

在有向连通图中，有且仅有一个顶点满足入度比出度少1，存在一个顶点出度小于入度1，其余顶点的出度与入度相同，而在无向连通图中，有2个顶点是奇数度，其余顶点 都是偶数度。则欧拉路径存在。

同样的，在有向连通图中，如果所有顶点出度与入度相等，在无向连通图中，所有顶点的度都是偶数度，则欧拉回路存在。

接下来我们来看一条欧拉回路的竞赛题目。

例1．圆周上有个点，,其中任意2点都用线段连接，能否一笔画出所有这些线段，使得第一条线段的终点和第二条线段的起始点相重合，第二条线段的终点和第三天线段的起始点相重合，依次类推，直到最后一条线段的终点和最初的一条线段的起始点相重合。

解题步骤：

圆周上有n个点，我们将它们视作顶点，且任意的2个点相连可以表示成2个顶点接触，得到一个阶的完全图,完全图中每个顶点的度都是,当为奇数，中的每个顶点都为偶顶点，所以根据判定条件，完全图中存在欧拉回路，从中的某个顶点开始，只要按照欧拉回路的顺序，依次连接整个图,最后回到原点就可以了，而当为偶数，中每个顶点都是奇顶点，包含欧拉回路，那么就不能一笔连接所有顶点了。

问题总结：这类问题就是判断图形中是否有欧拉回路，再通过作图观察各个顶点的出入度，结合定理出入度的判定，来得出结论，是否可以一笔画画出。

3.2汉密尔顿圈在数学竞赛中的应用：

汉密尔顿圈的概念：1859年，汉密尔顿提出了一个情形，在一个实心的正十二面体的顶点上，写满二十个城市的名字，是否能找到一条路线，使得他可以从某个城市出发，沿着这个十二面体的棱行进，恰好可以经过每个城市一次，并且最后再回到原点？这就是汉密尔顿圈的原型。

定理3.2.1 设是阶简单图，如果对图G中任意两个不相邻顶点u和v，均有

,

则图是汉密尔顿圈。

定理3.2.2 设是阶简单图，,如果对每个，,图G中度不超过的顶点个数小于，而且当n为奇数时，图G中度至多为的顶点个数不超过，则图是汉密尔顿圈。

虽然人们通过研究得出了一些定理可以判断出一些情形下是否存在汉密尔顿圈，不过，通常情况下，我们还是无法正确判断汉密尔顿圈是否存在。

例2.传说英国有一位国王，叫亚瑟王，他在王宫中召见他的2n名骑士，其中某些骑士之间互有恩怨，已知每名仇人不超过个，证明亚瑟王的谋士摩尔林一定有办法让这2n名骑士围着圆桌入座，使得每名骑士都不和他的仇人坐在一起。（波兰数学竞赛试题）

解题过程：

假设2个顶点A和B代表2个骑士,当且仅当AB不坐在一起时，令A和B相邻，我们作一个阶为的图G，由题意得，任何一名骑士他的仇人都少于n-1个,我们可以看做图G的顶点度数大于等于n,由定理可知，图G是一个汉密尔顿回路，问题就可以转换成让这2n名骑士按照这个汉密尔顿回路顶点的顺序依次入座就可以了，本题得解。

例3.有n 个人，围圆周入座，n,证明，可以调整这个人的座位，使得每个人的两旁就座的是原来不坐在一起的人（“祖冲之杯”邀请赛试题）

解题过程：

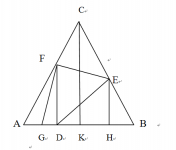
我们先假设围着圆桌入座的n个人按照逆势针入座，顺序为,,,(如图（3）)，再将,,,看做个顶点，假设2个顶点A和B,当且仅当AB不坐在一起时，令A和B相邻，我们可以得到一个阶简单图，中每个顶点的度是,时，,由定理可以得到图有汉密尔顿回路。所以问题就转变成了，让这n个人照着汉密尔顿回路的顶点入座就可以了，当,令5个人按照顶点顺序入座（如图（4））。

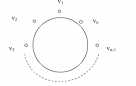
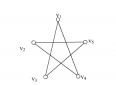
图（4）

图（3）

例4. 以一些圆盘覆盖平面上给定的个点。证明：若每个圆至少覆盖个点，则，任意两个点能有平面上的一条折线所连接，而这条线段整个的被一些圆所覆盖。（1966年第六届全俄数学奥林匹克）

证明：把这个点看做顶点，若存在一个圆，覆盖了2个顶点，那么在这2个顶点之间画一条边，作出图，中顶点的度必须大于n，如果每条边都能画出来，就表明它被一个圆覆盖，问题就转换成了证明图是连通图，如果图不是连通图，那么就存在一个连通分支，至多含有个顶点，这样对中的每个顶点，都有,与题意矛盾，从而是连通图。

问题总结：汉密尔顿回路问题在数学竞赛中通常以证明题的形式出现，既然是证明题，我们可以采用反证法，假设某种情况，并把问题中的情形用图形画出来，利用图形加以判断。如果能找出矛盾点，那么问题通常也能够迎刃而解。

3.3匹配问题在数学竞赛中的应用

匹配的概念：设是阶简单图，为图的某些边构成的集合，如果集合中任意的两条边都没有公共端点，那么集合称为图的一个边无关集，设和是图的顶点，如果和恰好是的某条边的两个端点，那么我们就说顶点和在边无关集下是匹配的。如果图的顶点M的某条边的端点，则顶点称为饱和的。设是图的一个匹配，如果不能再添加图的边e，使得是图G的匹配，则叫做图的极大匹配，对于图的一个匹配，如果图的每个顶点都是饱和的，则叫做图的完美匹配。匹配理论的中心问题是判断一个简单图G它是否存在完美匹配，而在匹配理论中研究的主要对象是二部分图。

设G是二部分图，把图的顶点集合分成2部分，，其中中顶点之间以及中顶点之间都不连边，如果图中有匹配，使中每个顶点都是饱和的，也就是说，中每个顶点在下部和中顶点匹配，则说可以匹配到中。下面引入2条定理。

定理3.3.1，对于的子集，用表示图G中所有与集合A的顶点相邻的顶点集合，即=,则集合X可以匹配到集合中的必要且充分条件是，对于每个是X的子集，均有（这里A表示集合A中顶点的个数）。

定理3.3.2二部分图G具有完美匹配的必要且充分条件是：,并且对每个子集A是X的子集均有。

例5某个网球俱乐部有20名成员，安排了14场比赛，每场比赛两名成员参加，每名成员至少安排一场比赛，证明，其中必有6场比赛，参赛者为12名不同的成员。（第18届美国数学奥林匹克试题）

解题思路:

我们把俱乐部的成员看成顶点，集合记做，顶点，当且仅当成员和比赛过时，令顶点和相邻，可以作一个20阶的简单图，由于一共进行了14场比赛，所以图G恰有14条边，而每位成员至少安排一场比赛，所以图中每个顶点都至少可以画一条边，即度至少是1，问题转换成，图是否至少含有6条边，且其中任意两条边都没有公共端点，换句话说，图G具有匹配（或边无关集），它至少含有6条边。

设是图的任意一个极大匹配，它含有条边，前面提到过，图G的极大匹配总是存在的，由于，匹配中任意2条边都不存在公共的端点，因此，被饱和的顶点有个，图含有20个顶点，所有余下有个顶点，这些点中任意2个不相邻，否则将相邻的边添加到，得到边子集，是图G的匹配，和是图的极大匹配相矛盾，因此，余下的个顶点中任意2个都不相邻，由已知条件，这些顶点中每一个都至少连有一条边，所有至少有条边不属于，于是图G中至少含有条边。因此由

.则，

剩余内容已隐藏，请支付后下载全文，论文总字数：14161字

相关图片展示：