论文总字数：14472字

目 录

摘要 1

Abstract 2

1.引言 3

1.1 研究背景和意义 3

1.2 国内外研究现状 3

2.牛顿迭代误差公式 4

2.1 牛顿迭代法的介绍 4

2.2 牛顿迭代法的收敛性定理及证明 5

2.3 牛顿迭代法的计算步骤 7

2.4牛顿迭代法应用举例 7

2.5牛顿迭代法的优缺点 8

3.区间牛顿迭代法 8

3.1 区间算术 8

3.2一维的区间牛顿方法 9

3.2.1 方法解释 9

3.2.2 迭代过程 10

3.2.3 图形解释 10

4. 程序求解实例 11

4.1用最大误差公式求解 11

4.1.1 求特定函数的最大误差公式 11

4.1.2 牛顿迭代误差与最大误差的比较 12

4.2 用一维的区间牛顿方法求解 12

5.结论 13

参考文献 13

致谢 15

精度可控的牛顿迭代法

严思远

，China

Abstract：The research in this dissertation is how to find the formula to make the Newton iteration method controllable in the iterative process, This will show how many iterations can be accurate enough to meet the need and get easy and efficient solution. In order to control the precision, we can start from the process of proving the convergence of Newton's iteration method, estimate the scope of the solution in advance and then the maximum error range is derived in the inequality, ie the formula. If the formula is continuously converged, the accuracy will continue to increase, which will meet the requirements of the accuracy of the solution. A maximum error formula can be obtained from the inequality that proves the convergence process of the Newton iteration method under the Lipschitz condition,which is effective by verificating.

Key words: Newton iteration method, convergence, controllable、Lipschitz

1.引言

1.1 研究背景和意义

误差存在于任何一个当今的科学领域，无论是物理测量还是估值运算都会产生各种误差，因此严格控制误差累积已成为计算数学和计算机科学的一项根本任务^[1]。我们知道，一个极小的误差带来的灾难或许是恐怖的，在这里可以看一个例子。1991年海湾战争中爱国者导弹阻拦飞毛腿导弹失败（导弹是由火箭搭载的）。单次误差为0.000000095（小数点后第八位出现错误），积累100小时后误差0.34秒，结果是拦截偏差六百米。单次误差看起来可能微不足道，但累积起来的偏差足以左右一场战争。更加直观的，我们知道指数爆炸，如果一个数字由1变为1.01，经过100次的累乘误差将达到1.7之多，这对于精确值1来说误差不可谓不大。牛顿方法是公式的多次迭代，为避免误差过大而影响到计算结果，牛顿迭代法的误差控制尤为重要。

牛顿迭代法也称为“牛顿法”，是根据 Isaac Newton在研究《运用无穷多方程的分析学》^[2](写于1669年，John Colson于1736年出版)对一个方法特例的描述中派生的。但是，他的方法与一般认为的现代方法有很大不同：Newton仅将该方法应用于多项式。他不计算一系列的近似值，而是计算一系列多项式，并且只在最后求出根的近似值。最后，Newton认为这种方法纯粹是代数的，并没有提到与微积分的联系。Newton可能是从Vieta的类似的但不太精确的方法中推导出他自己的方法。Vieta的方法的本质可以在波斯数学家 Sharaf al-Din al-Thsi的工作中找到，而他的继任者Jamshīdal-Kāshī使用牛顿法的一种形式求解来找到N的根（Ypma 1995）。Newton用于计算平方根的方法的一个特例早已为人所知，通常称为Babylonian方法。

尽管牛顿法和微积分毫无联系，它还是被17世纪的日本数学家SekiKōwa用来求解单变量方程。牛顿法于1685年首次发表于John Wallis的 《历史与实践代数论》。1690年，Joseph Raphson发表了对《通用方程分析》的简单描述。Raphson再次看到牛顿法纯粹作为一个代数方法仅被限制做多项式的应用，因此他描述了牛顿法中在逐次逼近方面的作用而不是像Newton那样用多项式做更复杂的序列。最后在1740年 Thomas Simpson将牛顿方法描述为用微积分求解一般非线性方程的迭代方法，基本上给出了如今为人们所知的描述。在同一刊物中，Simpson还推广到两个方程的系统，并指出牛顿法可用于通过将梯度设置为零来解决优化问题。Arthur Cayley于1879年在牛顿-傅立叶假想问题中首次注意到将牛顿法推广到最高次数大于2的多项式的复根和复数初始值的困难，这为研究有理函数迭代理论打开了通路。

1.2 国内外研究现状

牛顿迭代法存在一些缺陷，它并不是整体收敛的，在远离精确解时，牛顿迭代的方向不一定是误差下降方向——而目标函数值误差下降方向就是最优化努力的方向，因此人们先后通过一些方法来改进和修正牛顿迭代法。阻尼牛顿法是其中一个重要方法，它最核心的一点在于可以修改每次迭代的步长，通过沿着牛顿法确定的方向一维搜索最优的步长，最终选择使得函数值最小的步长。只要满足了“适用于精确线性搜索算法”的收敛性定理的条件，牛顿法的整体收敛性就得到了保证。但前提是非线性方程组的迭代矩阵正定，于是就出现了Goldstein-Price修正。Goldstein和Price提出如果矩阵不正定（此时难以给出解），就用“最速下降方向”来作为搜索方向。与以上的Goldstein-Price修正的思路不同，Goldfeld在1966年提出了另一种方法，其方法虽然还是在搜索方向上作处理，但是当迭代矩阵不正定时，他并非以最速下降方向来作为搜索方向，而是修正成一般的下降方向。但Goldfeld修正没有解决的问题是：难以给出选择下降方向的有效方法，实用性较差。之后还出现了Gill-Murray的Cholesky分解法和信赖域牛顿法。这些改进和修正都为牛顿迭代法的发展作出了贡献。

2.牛顿迭代误差公式

2.1 牛顿迭代法的介绍

牛顿迭代法（Newton's method）也被称为牛顿-拉夫逊（拉弗森）方法（Newton-Raphson method），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程根的方法。多数方程没有精确的求根方法，因此需要寻求其它解决方案来求得它的近似根。牛顿方法使用函数的泰勒级数的前几项来解析方程的根。牛顿迭代法是求复杂方程根的主要方法之一，它的最大优点在于在方程的单根附近具有平方收敛的性质，而且该法还可以用来求解方程的重根、复根，此时它是线性收敛的，但是可以通过一些方法变成超线性收敛。另外该方法因迭代式较易于求得，所以被广泛用于计算机编程中。

对于方程，如果是线性函数，则它的求根是非常容易的。牛顿法实质上是

一种线性化方法，其基本思想是将非线性方程逐步归结为某种线性方程求解。

设是一个函数的零点，若是一次或二次函数可直接求得，但是更一般的函数无法通过一般方法获得。这时可设点为其根的近似值，并作切线与轴相交，交点横坐标为，找到点，继续作切线交轴于，通过继续做切线找交点不断重复，这个点会越来越接近并收敛于的根。

我们可以作图直观观察，如图2.1.1

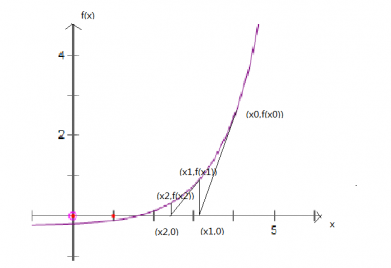
图 2.1.1 牛顿迭代示意图

通过点的切线L可求得

重复以上过程,可以得到

由于这种几何背景，牛顿法亦称为切线法。

除此之外，也可通过泰勒公式得到牛顿迭代公式。通过泰勒公式将从点处展开^[3]，得到

(2.1.3)

取线性部分

(2.1.4)

令,当时，则有 ，同样的可得到一阶线性的牛顿迭代公式(2.1.2)。

2.2 牛顿迭代法的收敛性定理及证明

定义2.2.1 设函数有不动点，若存在,使存在，则称迭代法是收敛的，如果存在的某个邻域R:，对任意,迭代法产生的序列收敛到，则称迭代法是局部收敛的。

定义2.2.2 设迭代法产生的序列收敛于方程的根,迭代误差为，若当时有渐近关系式(常数C)，则称该迭代过程是p阶收敛的，迭代过程的收敛速度p是指在迭代的收敛过程中，迭代误差的下降速度。 当时称为线性收敛，称为超线性收敛，成为平方收敛或二次收敛。

定理2.2.1 设函数满足,且在的邻域内有二阶连续导数，则当初值足够接近，由牛顿迭代公式得到的序列至少是二阶收敛的，并且有

(2.2.1)

当是单根时，牛顿迭代法至少是局部二阶收敛的。

该定理需要研究二阶导数的性质，是很困难的。因此有必要将该定理条件中的“在的邻域内有二阶连续导数”这个很强的限制条件进行弱化。

定义2.3.3 若存在正常数L，对任何有

剩余内容已隐藏，请支付后下载全文，论文总字数：14472字